§ 43. Деревья
Что такое дерево?
Как вы знаете из учебника 10 класса, дерево — это структура, отражающая иерархию (отношения подчинённости, многоуровневые связи). Напомним некоторые основные понятия, связанные с деревьями.
Дерево состоит из узлов и связей между ними (они называются дугами). Самый первый узел, расположенный на верхнем уровне (в него не входит ни одна стрелка-дуга), — это корень дерева. Конечные узлы, из которых не выходит ни одна дуга, называются листьями. Все остальные узлы, кроме корня и листьев, — это промежуточные узлы.
Из двух связанных узлов тот, который находится на более высоком уровне, называется родителем, а другой — сыном. Корень — это единственный узел, у которого нет родителя; у листьев нет сыновей.
Используются также понятия «предок» и «потомок». Потомок какого-то узла — это узел, в который можно перейти пострелкам от узла-предка. Соответственно, предок какого-то узла — это узел, из которого можно перейти по стрелкам в данный узел.
В дереве на рис. 6.11 родитель узла Е — это узел В, а предки узла Е — это узлы А и В, для которых узел Е — потомок. Потомками узла А (корня дерева) являются все остальные узлы.
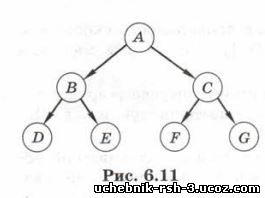 Высота дерева — это наибольшее расстояние (количество дуг) от корня до листа. Высота дерева, приведённого на рис. 6.11, равна 2.
Высота дерева — это наибольшее расстояние (количество дуг) от корня до листа. Высота дерева, приведённого на рис. 6.11, равна 2.
Формально дерево можно определить следующим образом:
- пустая структура — это дерево;
- дерево — это корень и несколько связанных с ним отдельных
(не связанных между собой) деревьев.
Здесь множество объектов (деревьев) определяется через само это множество на основе простого базового случая (пустого дерева). Такой приём называется рекурсией {см. главу 8 учебника для 10 класса). Согласно этому определению, дерево — это рекурсивная структура данных. Поэтому можно ожидать, что при работе с деревьями будут полезны рекурсивные алгоритмы.
Чаще всего в информатике используются двоичные (или бинарные) деревья, т. е. такие, в которых каждый узел имеет не более двух сыновей. Их также можно определить рекурсивно.
Деревья широко применяются в следующих задачах:
- поиск в большом массиве не меняющихся данных;
- сортировка данных;
- вычисление арифметических выражений;
- оптимальное кодирование данных (метод сжатия Хаффмана).
Деревья поиска
Известно, что для того, чтобы найти заданный элемент в неупорядоченном массиве из N элементов, может понадобиться N сравнений. Теперь предположим, что элементы массива организованы в виде специальным образом построенного дерева, например как показано на рис. 6.12.
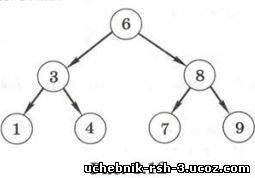
Значения, связанные с узлами дерева, по которым выполняется поиск, называются ключами этих узлов (кроме ключа узел может содержать множество других данных). Перечислим важные свойства дерева, показанного на рис. 6.12:
- слева от каждого узла находятся узлы, ключи которых
меньше или равны ключу данного узла; - справа от каждого узла находятся узлы, ключи которых
больше или равны ключу данного узла.
Дерево, обладающее такими свойствами, называется двоичным деревом поиска.
Например, пусть нужно найти узел, ключ которого равен 4. Начинаем поиск по дереву с корня. Ключ корня — 6 (больше заданного), поэтому дальше нужно искать только в левом поддереве и т. д. Если при линейном поиске в массиве за одно сравнение отсекается 1 элемент, здесь — сразу примерно половина оставшихся. Количество операций сравнения в этом случае пропорционально \og2N, т. е. алгоритм имеет асимптотическую сложность O(logaJV). Конечно, нужно учитывать, что предварительно дерево должно быть построено. Поэтому такой алгоритм выгодно применять в тех случаях, когда данные меняются редко, а поиск выполняется часто (например, в базах данных).
Обход двоичного дерева
Обойти дерево — это значит "посетить" все узлы по одному разу. Если перечислить узлы в порядке их посещения, мы представим данные в виде списка.
Существуют несколько способов обхода дерева:
• КЛП — «корень - левый - правый» (обход в прямом порядке):
посетить корень обойти левое поддерево обойти правое поддерево
• ЛКП — «левый - корень - правый» (симметричный обход):
обойти левое поддерево
посетить корень
обойти правое поддерево
• ЛПК — «левый - правый - корень» (обход в обратном по
рядке):
обойти левое поддерево обойти правое поддерево посетить корень
Как видим, это рекурсивные алгоритмы. Они должны заканчиваться без повторного вызова, когда текущий корень — пустое дерево.
Рассмотрим дерево, которое может быть составлено для вычисления арифметического выражения (1 + 4) * (9 - 5) (рис. 6.13).
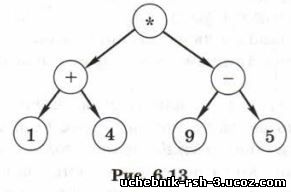
Выражение вычисляется по такому дереву снизу вверх, т. е. посещение корня дерева — это последняя выполняемая операция.
Различные типы обхода дают последовательность узлов:
КЛП: * + 1 4 - 9 5
ЛКП: 1+4*9-5
ЛПК: 14 + 95-*
В первом случае мы получили префиксную форму записи арифметического выражения, во втором — привычную нам инфиксную форму (только без скобок), а в третьем — постфиксную форму. Напомним, что в префиксной и в постфиксной формах скобки не нужны.
Обход КЛП называется «обходом в глубину», потому что сначала мы идём вглубь дерева по левым поддеревьям, пока не дойдём до листа. Такой обход можно выполнить с помощью стека следующим образом:
записать в стек корень дерева
нц пока стек не пуст
выбрать узел V с вершины стека
посетить узел V
если у узла V есть правый сын то
добавить в стек правого сына V
все
если у узла V есть левый сын то
добавить в стек левого сына V
все
кц
На рисунке 6.14 показано изменение состояния стека при таком обходе дерева, изображенного на рис. 6.13. Под стеком записана метка узла, который посещается (например, данные из этого узла выводятся на экран).
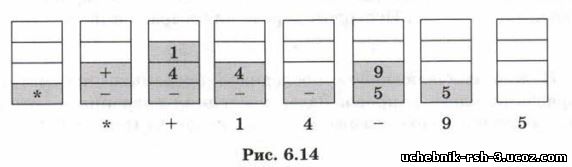
Существует ещё один способ обхода, который называют обходом в ширину. Сначала посещают корень дерева, затем — всех его сыновей, затем — сыновей сыновей («внуков») и т. д., постепенно спускаясь на один уровень вниз. Обход в ширину для приведённого выше дерева даст такую последовательность посещения узлов:
• + - 1 4 9 5
Для того чтобы выполнить такой обход, применяют очередь. В очередь записывают узлы, которые необходимо посетить. На псевдокоде обход в ширину можно записать так:
записать в очередь корень дерева нц пока очередь не пуста
выбрать первый узел V из очереди
посетить узел V
если у узла V есть левый сын то добавить в очередь левого сына V
все
если у узла V есть правый сын то добавить в очередь правого сына V
все
кц
Вычисление арифметических выражений
Один из способов вычисления арифметических выражений основан на использовании дерева. Сначала выражение, записанное в линейном виде (в одну строку), нужно «разобрать» и построить соответствующее ему дерево. Затем в результате прохода по этому дереву от листьев к корню вычисляется результат.
Для простоты будем рассматривать только арифметические выражения, содержащие числа и знаки четырёх арифметических операций: + - * /. Построим дерево для выражения
40 - 2 * 3 - 4 * 5
Нужно сначала найти последнюю операцию, просматривая выражение слева направо. Здесь последняя операция — это второе вычитание, оно оказывается в корне дерева (рис. 6.15).
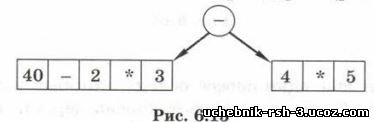
Как выполнить этот поиск в программе? Известно, что операции выполняются в порядке приоритета (старшинства): сначала операции с более высоким приоритетом (слева направо), потом — с более низким (также слева направо). Отсюда следует важный вывод.
В корень дерева нужно поместить поспеднюю из операций с наименьшим приоритетом.
Теперь нужно построить таким же способом лез поддеревья (рис. 6.16).
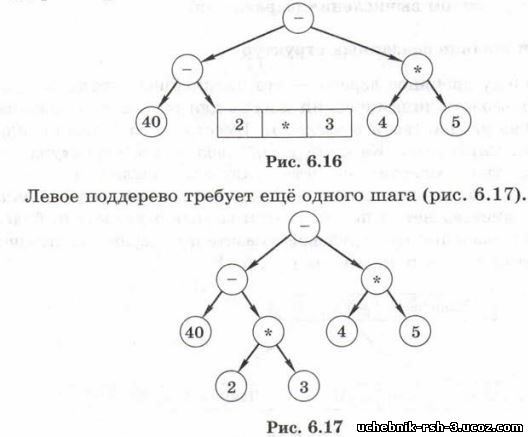
Эта процедура рекурсивная, её можно записать в виде псевдокода:
найти последнюю выполняемую операцию
если операций нет то
создать узел-лист
выход
все
поместить найденную операцию в корень дерева
построить левое поддерево
построить правое поддерево
Рекурсия заканчивается, когда в оставшейся части строки нет ни одной операции, значит, там находится число (это лист дерева).
Теперь вычислим выражение по дереву. Если в корне находится знак операции, её нужно применить к результатам вычисления поддеревьев:
nl:=значение левого поддерева
п2:=значение правого поддерева
результат:=операция(nl,п2)
Снова получился рекурсивный алгоритм.
Возможен особый случай (на нём заканчивается рекурсия), когда корень дерева содержит число (т. е. это лист). Это число и будет результатом вычисления выражения.
Использование связанных структур
Поскольку двоичное дерево — это нелинейная структура данных, использовать динамический массив для размещения элементов не очень удобно (хотя возможно). Вместо этого будем использовать связанные узлы. Каждый такой узел — это структура, содержащая три области: область данных, ссылка на левое поддерево (указатель) и ссылка на правое поддерево (второй указатель). У листьев нет сыновей, в этом случае в указатели будем записывать значение nil (нулевой указатель). Дерево, состоящее из трёх таких узлов, показано на рис. 6.18.
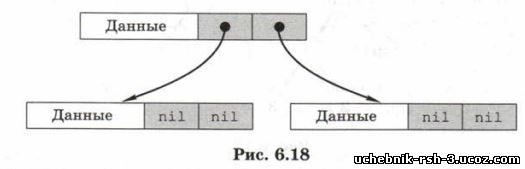
В данном случае область данных узла будет содержать одно поле — символьную строку, в которую записывается знак операции или число в символьном виде.
Введём два новых типа: TNode — узел дерева, и PNode — указатель (ссылку) на такой узел:
type
PNode = "TNode;
TNode = record
data: string[20];
left, right: PNode
end;
Самый важный момент — выделение памяти под новую структуру. Предположим, что р — это переменная-указатель типа PNode. Для того чтобы выделить память под новую структуру и записать адрес выделенного блока в р, используется процедура
New (англ. new — новый):
New(p);
Как программа определяет, сколько памяти нужно выделить? Чтобы ответить на этот вопрос, вспомним, что указатель р указы-вает на структуру типа TNode, размер которой и определяет раз-мер выделяемого блока памяти.
Для освобождения памяти служит процедура Dispose (англ. dispose — ликвидировать):
Dispose(p);
В основной программе объявим одну переменную типа PNode — это будет ссылка на корень дерева:
var T: PNode;
Вычисление выражения сводится к двум вызовам функций:
T:=Tree(s);
writeIn('Результат: ', Calc (Т) ) ;
Здесь предполагается, что арифметическое выражение записано в символьной строке s, функция Tree строит в памяти дерево по этой строке, а функция Calc — вычисляет значение выражения по готовому дереву.
При построении дерева нужно выделять в памяти новый узел и искать последнюю выполняемую операцию — это будет делать функция LastOp. Она возвращает О, если ни одной операции не обнаружено, в этом случае создаётся лист — узел без потомков. Если операция найдена, её обозначение записывается в поле data, а в указатели записываются адреса поддеревьев, которые строятся рекурсивно для левой и правой частей выражения:
function Tree(s: string): PNode;
var k: integer;
begin
New(Tree); (выделить память}
k:=LastOp(s);
if k=0 then begin {создать лист}
Tree'.data:=s;
Tree',left:=nil;
Tree".right:=nil;
end
else begin {создать узел-операцию}
Tree",data:=s[k);
Tree".left:=Tree(Copy(s,1,k-1));
ТгееЛ.right:=Tree(Copy(s,k+1,Length(s)-k))
end
end;
Функция Calc тоже будет рекурсивной:
function Calc(Tree: PNode) : integer,
var nl, n2, res: integer;
begin
if Tree-4, left = nil then
Val(Tree".data, Calc, res) else begin
nl:=Calc(ТгееЛ.left);
n2:=Calc(Tree".right);
case Tree^.data[1] of
'+': Calc:=nl+n;
'-': Calc:=nl-n2; 1
'*': Calc:=nl*n2;
'/': Calc:=nl div n2;
else Calc:=MaxInt end
end
end;
Если ссылка, переданная функции, указывает на лист (нет левого поддерева), то значение выражения — это результат преобразова-ния числа из символьной формы в числовую (с помощью процеду¬ры Val). В противном случае вычисляются значения для левого и правого поддеревьев и к ним применяется операция, указанная в корне дерева. В случае ошибки (неизвестной операции) функ¬ция возвращает значение Maxlnt — максимальное целое число.
Осталось написать функцию LastOp, Нужно найти в символь-ной строке последнюю операцию с минимальным приоритетом. Для этого составим функцию, возвращающую приоритет опера¬ции (переданного ей символа):
function Priority(op: char): integer;
begin
case op of
'+','-': Priority:=1;
'*','/': Priority:=2;
else Priority:=100
end
end;
Сложение и вычитание имеют приоритет 1, умножение и деле¬ние — приоритет 2, а все остальные символы (не операции) — приоритет 100 (условное значение).
Функция LastOp может выглядеть так:
function LastOp(s: string): integer;
var 1, minPrt: integer;
begin
minPrt:=50;
LastOp:=0;
for i:=l to Length(s) do
if Priority(s[i])<=minPrt then begin
minPrt:=Priority(s[i]);
LastOp:=i
end
end;
Обратите внимание, что в условном операторе указано нестрогое неравенство, чтобы найти именно последнюю операцию с наименьшим приоритетом. Начальное значение переменной minPrt можно выбрать любое между наибольшим приоритетом операций (2) и условным кодом не-операции (100). Тогда если найдена любая операция, условный оператор срабатывает, а если в строке нет операций, условие всегда ложно и в переменной LastOp остается начальное значение 0.
Хранение двоичного дерева в массиве
Двоичные деревья можно хранить в (динамическом) массиве почти так же, как и списки. Вопрос о том, как сохранить структуру (взаимосвязь узлов), решается следующим образом. Если нумерация элементов массива А начинается с 1, то сыновья элемента A[i] — это A[Z*i] и AJS4+1}. На рисунке 6.19 показан порядок расположения элементов в массиве для дерева, соответствующего выражению
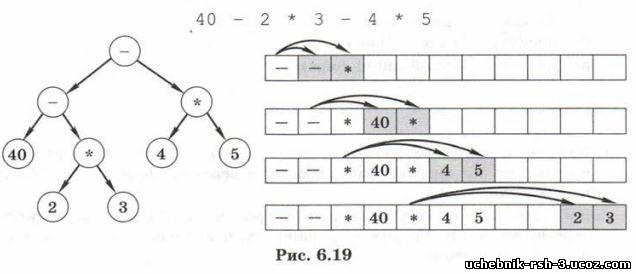
Алгоритм вычисления выражения остаётся прежним, изменяется только метод хранения данных. Обратите внимание, что некоторые элементы остались пустыми, это значит, что их родитель — лист дерева.