В начале главы мы отмечали принципиальное различие между вещественными и целыми числами: целые числа дискретны, а вещественные, напротив, непрерывны, а значит, не могут быть полностью корректно перенесены в дискретную по своей природе вычислительную машину. Как же всё-таки кодируются в компьютерах вещественные числа?
В первых ЭВМ использовалось кодирование с фиксированной запятой. Это значит, что положение запятой, отделяющей целую часть от дробной, было жёстко закреплено в
разрядной сетке конкретной ЭВМ — раз и навсегда для всех чисел и для всех технических устройств этой машины. Все вычислительные алгоритмы были заранее «настроены» на это фиксированное размещение. Но в задачах, которые решаются на компьютерах, встреча¬ются самые разнообразные по величине числа, от размера атома до астрономических расстояний. Чтобы согласовать их с таким жёстким представлением, программист, подготавливая задачу к решению на ЭВМ, выполнял большую предварительную работу по масштабированию данных: маленькие числа умножались на определённые коэффициенты, а большие, напротив, делились. Масштабы подбирались так, чтобы результаты всех операций, включая промежуточные, не выходили за пределы разрядной сетки и в то же время обеспечивалась максимально возможная точность (все разряды данных по возможности находились в пределах сетки). Эта работа требовала много времени и часто являлась источником ошибок.
Тем не менее работа с фиксированным размещением запятой не только показала недостатки метода, но и наметила путь их устранения. В самом деле, если наиболее сложным и трудоёмким местом является масштабирование данных, надо его автоматизировать. Иными словами, надо научить машину самостоятельно размещать запятую так, чтобы числа при счёте не выходили за разрядную сетку и по возможности сохранялись с максимальной точностью. Конечно, для этого нужно разрешить компьютеру «перемещать» запятую, а значит, дополнительно как-то сохранять в двоичном коде числа информацию о ее текущем положении. В этом и заключается главная идея представления чисел с плавающей запятой1.
Удобное представление вещественных чисел не пришлось специально придумывать. В математике уже существовал подходя¬щий способ записи, основанный на том, что любое число А в сис¬теме счисления с основанием В можно записать в виде
A=±ZBP,
где Z называют значащей частью, а показатель степени Р — порядком числа (рис. 4.19). Для десятичной системы это выглядит привычно, например, заряд электрона равен -1,6 ■ 10~19 кулона, а скорость света в вакууме составляет 3 ■ 108 м/с.
Однако представление числа с плавающей запятой не един¬ственно. Например, число 23,4 можно записать следующими способами:
2340 • 10-2 - 234 ■ 10-1 = 23,4 -10° = 2,34 ■ 101 -= 0,234 ■ 102 = 0,0234 ■ 103 = ...
На первый взгляд, выбор очень широкий, однако большинство вариантов обладают серьезными недостатками. В частности,
В англоязычных странах используется термин floating point - плавающая точка, поскольку в этих странах традиционно целая часть отделяется от дробной не запятой, как у нас, а точкой.
все представления,в которых значащая часть содержит нули непосредственно после запятой (2340, 23400 и т.п ) или перед ней ( 2340, 23400 и т.п) не подходят , поскольку, сохраняя эти незначащие нули, мы напрасно увеличиваем разрядность чисел. Согласно математической теории, для обеспечения максимальной точности при сохранении цифр числа в фиксированном количестве разрядов надо выбирать такой метод, при котором значащие цифры числа следует поместить как можно ближе к запятой. С этой точки зрения оптимальным будет вариант, когда целая часть равна нулю, а первая ненулевая цифра находится сразу после запятой (в нашем примере 0,234). При этом вместо двух частей (целой и дробной) остаётся только дробная, что фактически делает ненужной «разделительную» запятую.
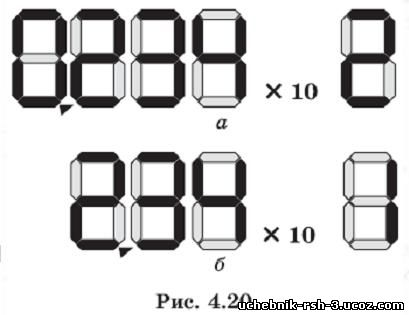
Но взгляните на рис. 4.20, а, изображающий такое число на индикаторе: первый разряд всегда равен нулю, что делает его практически бесполезным. Поэтому с точки зрения экономии разрядов лучше взять другой вариант, в котором значащая часть равна 2,34 (рис. 4.20, б). Именно такой выбор закреплён в стан¬дарте IEEE 7541, на котором основана арифметика вещественных чисел в современных компьютерах.
Итак, существуют два приблизительно равноценных способа представления чисел с плавающей запятой:
оптимальный с теоретической точки зрения, в котором це¬лая часть нулевая, а первая цифра дробной части ненулевая (0,234 ■ 102);
Последняя вереи. IEEE 754-2008.
- более удобный с практической точки зрения, в котором целая часть состоит из единственной ненулевой цифры (2,34 ■ 10')-
К сожалению, эта «двойственность» порождает некоторую путаницу. В теоретической литературе, как правило, используется первый способ1. Все описания конкретных компьютерных систем, напротив, базируются на втором. Причём в обоих случаях обычно используется один и тот же русский термин — мантисса. Зато в англоязычной компьютерной литературе приняты два разных термина: в первом случае значащая часть называется mantissa (слово «мантисса» для математиков однозначно связано с дробной частью числа), а во втором — significand (значащая часть).
Далее мы будем использовать второй вариант, поскольку именно он даёт возможность решать задачи, связанные с практическим кодированием вещественных чисел. В связи с этим мы будем применять термин «значащая часть», а не «мантисса».
В компьютере используется такое представление вещественных чисел с плавающей запятой, при котором значащая часть Z удовлетворяет условию 1 <Z <B, где В — основание системы счисления. Такое представление называется нормализованным.
Нормализованное представление числа единственно — в нашем примере это 2,34 ■ 101. Любое число может быть легко нор¬мализовано. Единственное, но важное исключение из правила составляет нуль — для него невозможно получить Z > 1. Ради такого важного случая было введено дополнительное соглашение: число 0, в котором все биты нулевые, в качестве исключения считается нормализованным.
Всё сказанное выше можно применить и к двоичной системе:
A = ±Z-2P, причём 1<Z<2.
Например: -710 = -111 ■ 2° = -1,11 ■ 210 (не забывайте, что значащая часть и порядок записаны в двоичной системе!); отсюда Z =1,11 и Р = 10. Двоичная значащая часть всегда (исключая, разумеется, ноль!) начинается с единицы, так как 1<Z<2. Поэтому
К этой группе относится большинство отечественных книг по основам вычислительной техники.
во многих компьютерах (в том числе в компьютерах на базе процессоров Intel) эта так называемая скрытая единица не хранится в ОЗУ, что позволяет сэкономить еще один дополнительный разряд значащей части1.
Идея «скрытой единицы» раньше действительно давала заметное увеличение точности представления чисел, поскольку количество разрядов в устройствах ЭВМ того времени было невелико и поэтому усложнение метода кодирования было оправдано. Сейчас, когда процессоры работают с 64-битными данными, это скорее дань традиции, чем практически полезная мера2.
Таким образом, при кодировании вещественного числа с плавающей запятой фактически хранятся две величины: его значащая часть (significand) и порядок. От разрядности значащей части зависит точность вычислений, а от разрядности порядка — диапазон представления чисел. В таблице 4.6 приведены характеристики стандартных вещественных типов данных, используемых в математическом сопроцессоре Intel.
Рассмотрим, как «распланированы» 4 байта, отводимые под простейший тип single. Тип double устроен совершенно аналогично, а тип extended, который является основным форматом для
1 В результате то, что осталось после «скрытия» единичной целой части/, можно вполне обоснованно называть мантиссой.
2 Оценим величину добавки для математического сопроцессора Intel. Значащая часть чисел двойной точности вместо скрытой «единицы»приобретает дополнительный 53-й (!) бит, что прибавляет к значению числа поправку 2-53≈ 1,1•10-16, влияющую на 16-й десятичный знак; согласно IEEE 754-2008, в 128-битовых числах эта поправка будет и того меньше : 2113≈9,6•1035
вычислений в математическом сопроцессоре, отличается только тем, что в нём единица в целой части не «скрывается».
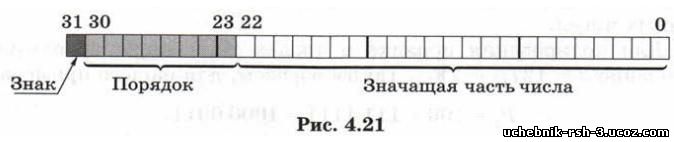
В числах типа single 23 младших бита (с номерами от О до 22) хранят значащую часть числа, следующие 8 битов (с 23 по 30) — порядок, а старший (31-й) бит отведен под знак числа (рис. 4.21).
Правила двоичного кодирования вещественных чисел во многом отличаются от правил кодирования целых чисел. Для того чтобы в них разобраться, рассмотрим конкретный пример — закодируем число -17,25 в формате single. Прежде всего, переведём модуль числа в двоичную систему, отдельно целую и дробную части (см. § 11):
17,25 = 10001,013.
Для нормализации нужно передвинуть запятую на 410 = 1002
10001,01 ■ 2° = 1,000101 ■ 2100.
Построим значащую часть, «скрыв» единицу в целой части:
М = Z -1 = 0,0001010...0.
Так как число отрицательное, знаковый разряд нужно установить в 1, т. е. $=1
В отличие от целых чисел значащая часть вещественных чисел хранится в прямом коде.
Таким образом, значащие части положительного и равного по модулю отрицательного числа одинаковы, а отличаются они только старшим (знаковым) битом.
Теперь остаётся закодировать двоичный порядок 100. Порядок — это целое число со знаком, для него используется кодирование со смещением: чтобы вообще избавиться от знака порядка, к нему добавляют некоторое положительное смещение d:
Pd=P + d.
Величина смещения подбирается так, чтобы число Pd было всегда положительным. В этом случае оказывается легче скон¬струировать математический сопроцессор для обработки вещественных чисел.
Для кодирования порядка в числах типа single используют смещение d = 12710 = 7F16. Таким образом, для нашего примера
Pd = 100+ 111 1111 = 1000 0011.
Собирая теперь S, Pd и М в единое 32-разрядное число, полу¬чаем:
1 10000011 00010100000000000000000
или более компактно в шестнадцатеричной системе:
С1 8А 00 00.
Этот код и будет записан в память1.
Не все двоичные комбинации для вещественных чисел соответствуют «правильным »числам: некоторые из них кодируют бесконечные значения, а некоторые — нечисловые данные (англ. NaN — not a number, «не число»). Они отличаются от остальных чисел тем, что имеют максимально возможный порядок2 {например, для типа single это смещённый порядок Pd — 255, а для типа для double — 2047). Подобные «неправильные» данные возника¬ют только в результате ошибок в вычислениях.
Таким образом, мы увидели, что целые и вещественные числа хранятся в памяти компьютера совершенно по-разному. Поэтому неудивительно, что свойства значений, скажем 3 и 3,0, в компьютерной арифметике совершенно различные.
1 На самом деле в IBM-совместимых персональных компьютерах байты будут сохранены в памяти в обратном порядке: 00 00 8А С1.
2 Это вполне логично, поскольку для вещественных чисел переполнение (получение «бесконечного» значения) наступает именно при больших порядках.
Вопросы и задания
- Чем вызваны трудности, возникающие при представлении вещественных чисел в компьютере? Как они связаны с непрерывностью вещественных чисел в математике?
- Объясните, как хранятся вещественные числа с фиксированной запятой. Почему этот метод не используется в современных компьютерах?
- Что такое плавающая запятая? Из каких частей состоит число при кодировании с плавающей запятой?
- Приведите примеры физических величин, которые обычно записывают в форме с плавающей запятой.
- Почему метод представления чисел с плавающей запятой неоднозначен? Как изменится порядок, если запятую сместить на один разряд влево (вправо)?
- Что такое нормализованная форма записи числа?
- Как требования нормализации связаны с точностью представления вещественных чисел?
- Единственно ли нормализованное представление числа? Все ли числа имеют нормализованное представление?
- Почему старший бит значащей части нормализованного двоичного числа всегда равен единице? Как этот факт используется на практике?
- Какие числа сохраняются в памяти с нулевой значащей частью?
- На что влияет разрядность значащей части и разрядность порядка?
- Почему задание разрядности для целых чисел однозначно определяет их свойства, а для вещественных — нет?
- Что вы знаете о типах single, double и extended?
- Как хранится порядок во всех рассмотренных форматах вещественных чисел? Почему не хранится знак порядка?
- Сравните методы хранения отрицательных целых и вещественных чисел.
- Как по двоичному представлению вещественного числа определить, положительное оно или отрицательное? Подходит ли этот метод для целых чисел?
- В каком из вещественных форм не используется «скрытая единица» и почему?
18.Какие логические операции и с какой маской надо применить, чтобы в переменной типа single :
а) выделить значащую часть, сбросив порядок и знаковый бит;
б) восстановить в полученной знаковой части «скрытую единицу»?
19. Как можно выделить смещенный порядок из числа типа single? Как получить истинное значение порядка?
20. С помощью какой маски можно выделить знаковый бит числа, хранящегося в формате single?
21. Что такое NaN?
22. Чем различаются представление в памяти целого числа и равного ему вещественного с нулевой дробной частью ( например, 12 и 12,0)?
Подготовьте сообщение
а)«Типы данных для хранения вещественных чисел»
б)«Стандарт IEEE-754»