§42
Стек, очередь, дек
Что такое стек?
Представьте себе стопку книг (подносов, кирпичей и т. п.)-С точки зрения информатики, её можно воспринимать как список элементов, расположенных в определённом порядке. Этот список имеет одну особенность — удалять и добавлять элементы можно только с одной («верхней») стороны. Действительно, для того чтобы вытащить какую-то книгу из стопки, нужно сначала снять все те книги, которые находятся на ней. Положить книгу сразу в середину тоже нельзя.
Стек, очередь, дек
Стек (англ. stack — стопка) — это линейный список, в котором элементы добавляются и удаляются только с одного конца (англ. LIFO: Last In - First Out — последний пришёл — первым ушёл).
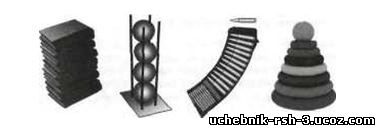
На рисунке 6.6 показаны примеры стеков вокруг нас, в том числе автоматный магазин и детская пирамидка.
Рнс. 6.6
Как вы знаете из учебника для 10 класса, стек используется при выполнении программ: в нём хранятся адреса возврата из подпрограмм, параметры, передаваемые функциям и процедурам, а также локальные переменные.
Задача I. В файле записаны целые числа. Нужно вывести их в другой файл в обратном порядке.
В этой задаче очень удобно использовать стек. Для стека определены две операции:
- добавить элемент на вершину стека (англ. push — втолкнуть);
- получить элемент с вершины стека и удалить его из стека (англ. pop — вытолкнуть).
Запишем алгоритм решения на псевдокоде. Сначала читаем данные и добавляем их в стек:
нц пока файл не пуст
прочитать х
добавить х в стек
кц
Теперь верхний элемент стека — это последнее число, прочитанное из файла. Поэтому остаётся «вытолкнуть» все записанные в стек числа, они будут выходить в обратном порядке:
нц пока стек не пуст
вытолкнуть число из стека в х
записать х в файл
кц
Использование динамического массива
Поскольку стек — это линейная структура данных с переменным количеством элементов, для создания стека в программе мы можем использовать динамический массив. Конечно, можно организовать стек из обычного (статического) массива, но его будет невозможно расширить сверх размера, выделенного при трансляции.
Для рассмотренной выше задачи 1 структура-стек содержит динамический целочисленный массив и количество используемых в нём элементов:

Будем считать, что стек «растёт» от начала к концу массива, т. е. вершина стека — это последний элемент.
Для работы со стеком нужны две подпрограммы:
- процедура Push, которая добавляет новый элемент на вершину стека;
- функция Pop, которая убирает его из стека.
Приведем эти подпрограммы
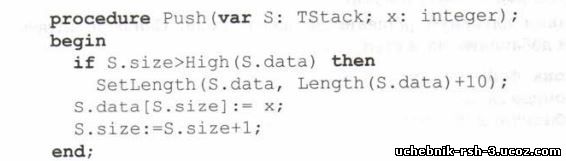
function Pop(var 5:TStack): integer;
begin
S.size:=S.size-l;
Pop:=S.data[S.size];
end;
Обратите внимание, что здесь структура типа TStack изменяется внутри подпрограмм, поэтому этот параметр должен быть изменяемым (описан с помощью var).
Заметим, что если нам понадобится стек, который хранит данные другого типа (например, символы, символьные строки или структуры), в объявлении типа и в приведённых подпрограммах нужно просто заменить integer на нужный тип.
Кроме того, введём процедуру Initstack, которая заполняет поля структуры начальными значениями (выполняет инициализацию стека):
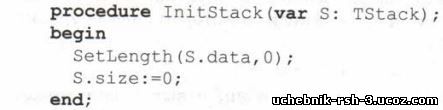
Здесь S — переменная типа TStack; F — файловая переменная, связанная с файлом, открытым на чтение; х — целая переменная. Вывод результата в файл выполняется так:
for i:=0 to S.size-1 do begin
x: = Pop(S); writeln(F, x) ;
end;
Здесь i — целая переменная, a F —■ файловая переменная, связанная с файлом, открытым на запись.
Вычисление арифметических выражений
Вы не задумывались, как компьютер вычисляет арифметические выражения, записанные в такой форме: (5+15)7(4+7-1)?
Такая запись называется инфиксной — в ней знак операции расположен между операндами (данными, участвующими в операции). Инфиксная форма неудобна для автоматических вычислений из-за того, что выражение содержит скобки и его нельзя вычислить за один проход слева направо.
В 1920 г. польский математик Ян Лукасевич предложил префиксную форму, которую стали называть польской нотацией. В ней знак операции расположен перед операндами. Например, выражение (5 + 15)/(4 + 7-1) может быть записано в виде
/ + 5 15- + 47 1.
Скобки здесь не требуются, так как порядок операций строго определён: сначала выполняются два сложения (+ 5 15 и + 4 7), затем вычитание, и, наконец, деление. Первой стоит последняя операция.
В середине 1950-х гг. была предложена обратная польская нотация, или постфиксная форма записи, в которой знак операции стоит после операндов:
5 15+47+1-/
В этом случае также не нужны скобки, и выражение может быть вычислено за один просмотр с помощью стека следующим образом:
- если очередной элемент — число (или переменная), он записывается в стек;
- если очередной элемент — операция, то она выполняется с
верхними элементами стека, и после этого в стек помещает
ся результат выполнения этой операции.
Покажем, как работает этот алгоритм (стек «растёт» снизу вверх) (рис. 6.7).
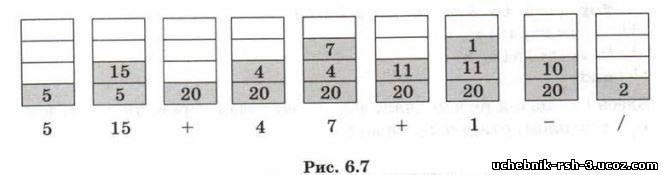
В результате в стеке остаётся значение заданного выражения.
Скобочные выражения
Задача 2. Вводится символьная строка, в которой записано некоторое (арифметическое) выражение, использующее скобки трёх типов: О, [] и {(. Проверить, правильно ли расставлены скобки.
Например, выражение ()[{{>[]]] — правильное, потому что каждой открывающей скобке соответствует закрывающая, и вложенность скобок не нарушается. Выражения
[( ) [ [ [ ( ) [ ( ) } ) ( ( [ ) ]
неправильные. В первых трёх есть непарные скобки, а в последних двух не соблюдается вложенность скобок.
Начнём с задачи, в которой используется только один вид скобок. Её можно решить с помощью счётчика скобок. Сначала счётчик равен нулю. Строка просматривается слева направо, если очередной символ — открывающая скобка, то счётчик увеличивается на 1, если закрывающая — уменьшается на 1. В конце просмотра счётчик должен быть равен нулю (все скобки парные), кроме того, во время просмотра он не должен становиться отрицательным (должна соблюдаться вложенность скобок).
В исходной задаче (с тремя типами скобок) хочется завести три счётчика и работать с каждым отдельно. Однако это решение неверное. Например, для выражения ({[)}] условия правильности выполняются отдельно для каждого вида скобок, но не для выражения в пелом.
Задачи, в которых важна вложенность объектов, удобно решать с помощью стека. Нас интересуют только открывающие и закрывающие скобки, на остальные символы можно не обращать внимания.
Строка просматривается слева направо. Если очередной символ — открывающая скобка, нужно поместить её на вершину стека. Если это закрывающая скобка, то проверяем, что лежит на вершине стека: если там соответствующая открывающая скобка, то её нужно просто снять со стека. Если стек пуст или на вершине лежит открывающая скобка другого типа, выражение неверное и нужно закончить просмотр. В конце обработки правильной строки стек должен быть пуст. Кроме того, во время просмотра не должно быть ошибок. Работа такого алгоритма иллюстрируется на рисунке (для правильного выражения) (рис. 6.8).
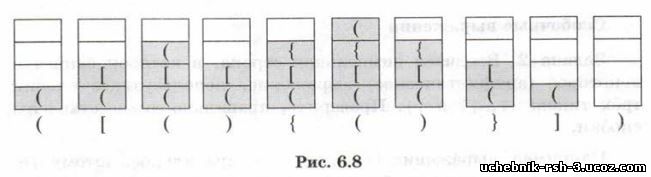
Введём следующие переменные:
type TStack=record
data: array of char;
size: integer;
end;
Отличие стека s от стека в предыдущей задаче только в том, что он содержит не целые числа, а символы (типа char). Поэтому приводить подпрограммы Push и Pop мы не будем, вы можете их переделать самостоятельно. Для удобства добавим только логическую функцию, которая возвращает значение True (истина), если стек пуст:
function isEmpty(S: TStack): boolean;
begin
isEmpty:=(S.size=0);
end;
Введём строковые константы L и R, которые содержат все виды открывающих и соответствующих закрывающих скобок:
const L = ' ( [ { ' ;
R = ' ) ] } ' ;
Объявим переменные основной программы:
var S: TStack;
р, i: integer;
str: string;
err: boolean;
с: char;
Переменная str — это исходная строка. Логическая переменная err будет сигнализировать об ошибке. Сначала ей присваивается значение False («ложь»).
В основном цикле меняется целая переменная i, которая обозначает номер текущего символа, переменная р используется как вспомогательная:

Сначала мы ищем символ str[i] в строке L, т. е. среди открывающих скобок (строка 1). Если это действительно открывающая скобка, помещаем её в стек (2). Далее ищем символ среди закрывающих скобок (3). Если нашли, то в первую очередь проверяем, не пуст ли стек. Бели стек пуст, выражение неверное и переменная err принимает истинное значение. Если в стеке что-то есть, снимаем символ с вершины стека в символьную переменную с (6). В строке (7) сравнивается тип (номер) закрывающей скобки р и номер открывающей скобки, найденной на вершине стека. Если они не совпадают, выражение неправильное, и в переменную err записывается значение True. Если при обработке текущего символа обнаружено, что выражение неверное (значение переменной err — True), нужно закончить цикл досрочно с помощью оператора break (8).
В конце программы остаётся вывести результат на экран:
if not err
then writeln('Выражение правильное.')
else writeln('Выражение неправильное.');
Очереди, деки
Все мы знакомы с принципом очереди: первый пришёл — первый обслужен (англ. FIFO: First In — First Out). Соответствующая структура данных в информатике тоже называется очередью.
Очередь — это линейный список, для которого введены две операции:
- добавление нового элемента в конец очереди;
- удаление первого элемента из очереди.
Очередь — это не просто теоретическая модель. Операционные системы используют очереди для организации сообщений между программами: каждая программа имеет свою очередь сообщений. Контроллеры жёстких дисков формируют очереди запросов ввода и вывода данных. В сетевых маршрутизаторах создаётся очередь из пакетов данных, ожидающих отправки.
Задача 3. Рисунок задан в виде матрицы А, в которой элемент А[у, х] определяет цвет пикселя (х, у) на пересечении строки у и столбца х. Требуется перекрасить в цвет 2 одноцветную область, начиная с пикселя {х0, у0). На рисунке 6.9 показан результат такой заливки для матрицы из 5 строк и 5 столбцов с начальной точкой (2,1).
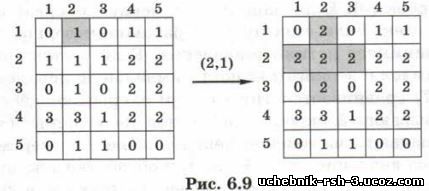
Эта задача актуальна для графических программ. Один из возможных вариантов решения использует очередь, элементы которой — координаты пикселей (точек):
добавить в очередь точку (х0,уо) запомнить цвет начальной точки нц пока очередь не пуста
взять из очереди точку (х,у)
если А[у,х]=цвету начальной точки то
А[у,х]:=2;
добавить в очередь точку (х-1,у)
добавить в очередь точку (х+1,у)
добавить в очередь точку (х,у-1)
добавить в очередь точку (х,у+1)
все
кц
Конечно, в очередь добавляются только те точки, которые находятся в пределах рисунка (матрицы А). Заметим, что в этом алгоритме некоторые точки могут быть добавлены в очередь несколько раз (подумайте, когда это может случиться). Поэтому алгоритм можно несколько улучшить, как-то помечая точки, уже добавленные в очередь, чтобы не добавлять их повторно (попробуйте сделать это самостоятельно).
Две координаты точки связаны между собой, поэтому в программе лучше объединить их в структуру TPoint (от англ. point — точка), а очередь составить из таких структур:
Type TPoint = record
х, у: integer;
end;
TQueue = record
data: array of TPoint;
size: integer
end;
Для удобства построим функцию Point, которая формирует структуру типа TPoint по заданным координатам:
function Point(x,у: integer): TPoint;
begin
Point.x:=x;
Point.у:=у
end;
Для работы с очередью, основанной на динамическом массиве, введём две подпрограммы:
- процедура Put добавляет новый элемент в конец очереди;
если нужно, массив расширяется блоками по 10 элементов; - функция Get возвращает первый элемент очереди и удаляет
его из очереди (обработку ошибки «очередь пуста» вы мо
жете сделать самостоятельно); все следующие элементы
сдвигаются к началу массива.
procedure Putfvar Q: TQueue; pt: TPoint);
begin
if Q.size > High(Q.data) then
SetLength(Q-data, Length(Q.data)+10);
Q.data[Q.size]:=pt;
Q. size:=Q.size+1
end;
function Get(var Q:TQueue): TPoint;
var i: integer;
begin
Get:=Q.data[0];
Q.size:=Q.size-l; for i:=0 to Q.Size-1 do
Q.data[i]:=Q.data[i+1]
end;
Остаётся написать основную программу- Объявляем константы и переменные:
const ХМАХ = 5; УМАХ = 5;
NEW_COLOR = 2;
var Q: TQueue;
xO, yO, color: integer;
A: array[1..YMAX,1..XMAX] of integer;
pt: TPoint;
Предположим, что матрица А заполнена. Задаём исходную точку, с которой начинается заливка, запоминаем её «старый» цвет и добавляем эту точку в очередь:
хО:=2; у0:=1; color:~A[yO,xO];
Put[Q,Point(хО,yO)) ;
Основной цикл практически повторяет алгоритм на псевдокоде:
while not isEmpty(Q) do begin
pt:=Get <Q);
if A[pt.y,pt.x]=color then begin
A[pt.y,pt.x]:=NEW_COLOR;
if pt.x>l then Put(Q,Point(pt.x-l,pt.y));
if pt.x<XMAX then Put(Q,Point(pt.x+1,pt.y));
if pt.y>l then Put(Q,Point(pt.x,pt.y-l));
if pt.y<YMAX then Put(Q,Point(pt.x,pt.y+l))
end
end;
Здесь функция isEmpty — такая же, как и для стека: возвращает True, если очередь пуста (поле size равно нулю).
В приведённом примере начало очереди всегда совпадает с первым элементом массива (имеющим индекс 0). При этом удаление элемента иа очереди неэффективно, потому что требуется сдвинуть все оставшиеся элементы к началу массива.Существует и другой подход, при котором элементы очереди не передвигаются. . Допустим, что мы знаем, что количечество элементов в очереди всегда меньше N. Тогда можно выделить статический массив из N элементов (с индексами от 1 до N) и хранить в отдельных переменных номера первого элемента очереди ( "головы", англ. head) и последнего элемента ("хвоста", англ. tail). На рисунке 6.10, a показана из 5 элеметов. В этом случае удаление элемента из очереди сводится просто к увеличению переменной Head (рис. 6.10,б).
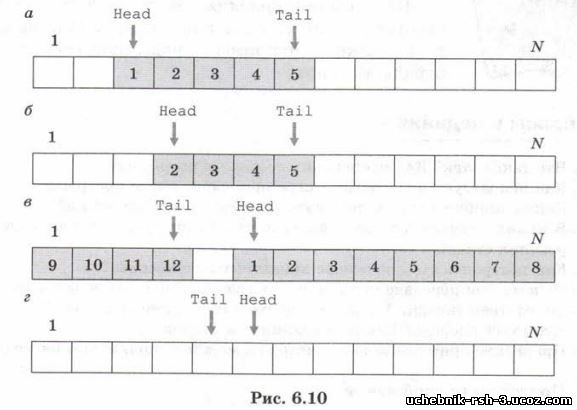
При добавлении элемента в конец очереди переменная Tail увеличивается на 1. Если она перед этим указывала на последний элемент массива, то следующий элемент записывается в начало массива, а переменной Tail присваивается значение 1. Таким образом, массив оказывается замкнутым «в кольцо*. На рисунке 6.10, в показана целиком заполненная очередь, а на рис. 6.10, г — пустая очередь. Один элемент массива всегда остаётся незанятым, иначе невозможно будет различить состояния «очередь пуста» и «очередь заполнена».
Отметим, что приведённая здесь модель описывает работу кольцевого буфера клавиатуры, который может хранить до 15 двухбайтных слов.
Кроме того, очередь можно построить на основе связного списка (см. § 41). Детали такой реализации можно найти в литературе или в Интернете.
Существует еще одна линейная динамическая структура данных, которая называется дек.
Дек — это линейный список, в котором можно добавлять и удалять элементы как с одного, так и с другого конца.
 Из этого определения следует, что дек может работать и как стек, и как очередь. С помощью дека можно, например, моделировать колоду игральных карт.
Из этого определения следует, что дек может работать и как стек, и как очередь. С помощью дека можно, например, моделировать колоду игральных карт.
К прошлому параграфу